Dielectric barrier discharge (DBD) plasma actuation on flow over cylinder

A Dielectric Barrier Discharge (DBD) plasma actuator uses electric fields to create a thin layer of plasma along a surface which induces a small but fast-moving wall jet that adds momentum to the airflow—without any moving parts. When energizing the boundary layer, plasma actuators can suppress vortex shedding, delay flow separation, and reduce drag around bluff bodies like circular cylinders. This makes them an effective, lightweight solution for controlling unsteady wakes in aerodynamic applications.

To simulate the effect of the plasma actuator on bluff-body flow, I used a CFD solver equipped with User-Defined Functions (UDFs) to prescribe time-dependent body forces near the cylinder wall. This allowed me to directly emulate the actuator’s behavior within the numerical model, treating the plasma-induced force as a localized momentum source applied in the near-wall region. I designed a UDF that let me vary multiple actuation parameters, including:

• Forcing amplitude (strength of the body force)

• Actuation frequency (how often the force is applied)

• Duty cycle (time fraction) (percentage of time the actuator is “on” within a period)

• Force direction and spatial extent (to target separation zones effectively)

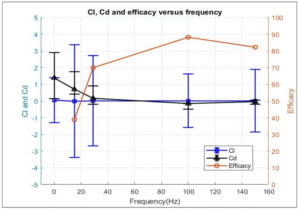
By conducting a comprehensive parametric sweep across these variables, I could observe how each setting influenced vortex shedding, wake stability, and drag behavior. The simulations revealed that the actuator’s effectiveness was highly sensitive to the chosen parameters—too strong or too frequent actuation could amplify unsteadiness, while well-tuned settings significantly suppressed vortex shedding, reduced lift fluctuations, and achieved measurable drag reduction. Ultimately, I identified an optimal control configuration that delivered the most efficient aerodynamic performance without requiring excessive energy input—demonstrating the potential of plasma actuators as a lightweight, responsive flow control strategy for real-world applications.

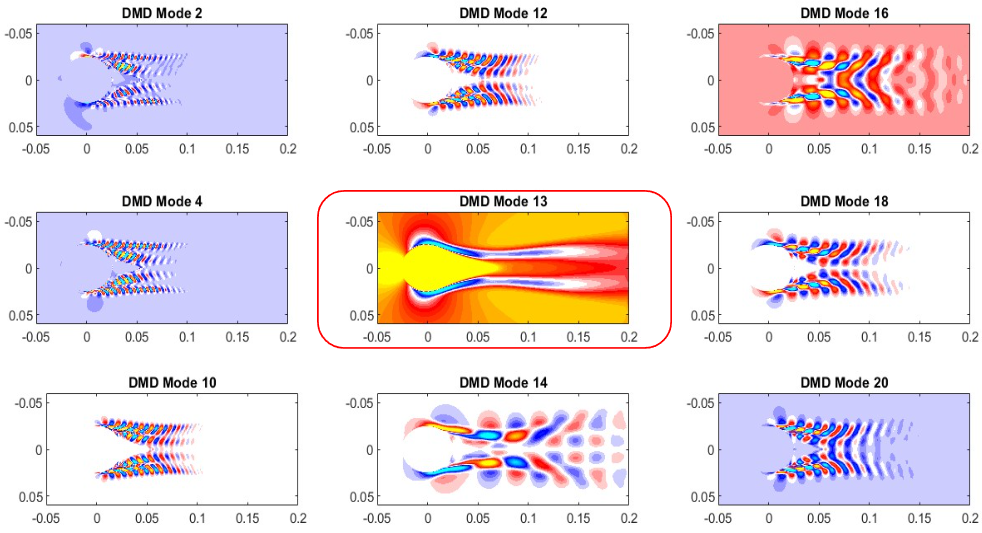
To better understand and predict the unsteady flow behavior, I applied Dynamic Mode Decomposition (DMD) and Proper Orthogonal Decomposition (POD) to the simulation data. These data-driven techniques helped extract dominant spatial and temporal patterns from the flow field, revealing coherent structures and their evolution over time.